Ha egy edényben levő folyadék a felszín alatt H mélységben levő oldalnyíláson át kifolyik az edényből, akkor a kiáramló folyadékra alkalmazhatjuk a Daniel Bernoulli (1700-1782), svájci fizikus által 1738-ban felállított híres Bernoulli-féle egyenletet.
            Ha az edény oldalán levő nyílás az edényhez képest igen kicsiny keresztmetszetű, akkor a felszín süllyedésének a sebessége gyakorlatilag zérusnak tekinthető

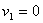
míg a nyílásnál a kifolyási sebesség legyen

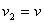
A folyadék felszínén és a kifolyási nyílásnál is a folyadék a külső levegővel érintkezik, így a nyomás megegyezik a külső nyomással, azaz

.

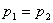Ha a koordináta rendszert a kifolyási nyíláshoz rögzítjük, akkor a folyadék felszínének magassága

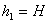
míg a kifolyás magassága

Felírva, majd egyszerűsítve a Bernoulli-féle egyenletet, adódik a folyadék kiömlési sebessége:

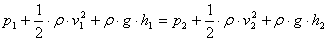
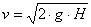
vagyis – a folyadék sűrűségétől függetlenül- a kiömlési sebesség akkora, mintha a kiömlő folyadék a H magasságból szabadon esett volna. Mivel ezt az összefüggést – a szökőkutak vizsgálata közben- már 1646-ban tapasztalati úton felismerte Evangelista Torricelli (1608-1647) olasz fizikus, ezt a tételt Torricelli tételének is nevezik.
            Kimutatható, hogy a Torricelli tétellel kiszámított sebességgel vízszintesen kilépő vízsugár a hajítás törvényeit követi és a vízsugárnak parabola alakja van. A vízsugár akkor jut a legmesszebbre, ha az edény nyílása a vízoszlop magasságának közepén van és azok a vízsugarak, amelyek a középső nyílástól fölfelé vagy lefelé egyenlő távolságra levő nyílásokból indulnak ki, egyenlő távolságra jutnak.
            A Torricelli-féle kiömlési törvényt és a fenti állításokat könnyen igazolhatjuk azzal az ún. Weisbach-féle kifolyási készülékkel, amely a nevét Julius Ludwig Weisbach (1806-1871) német mérnökről kapta. Ez az eszköz egy kb. 80 cm magas, széles bádogedény, amelynek oldalán négy olyan nyílás van, amelyeket külön-külön elzárhatunk egy-egy felcsiszolt sárgarézlappal. A nyílások lezárása után töltsük meg az edényt vízzel, majd az egyes nyílásokat sorra szabaddá téve (egyszerre mindig csak egy legyen nyitva) mérjük meg, a nyílások asztaltól mért magasságát

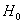
valamint azt, hogy milyen távolságban éri el az asztalt a kilövellő vízoszlop

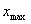
Számítsuk ki a

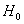
magasságból szabadon eső vízsugár esési idejét

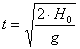
amelyet vízszintes hajítás távolságára vonatkozó összefüggésbe

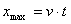
beírva, kiszámíthatjuk a vízsugár kezdeti vízszintes irányú kezdősebességét

Ha ez a sebesség megegyezik a Torricelli tétel segítségével kiszámított sebességgel,

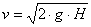
akkor a Torricelli tételt bebizonyítottuk.
            A kétféle számítás eredménye valamilyen mértékben biztosan eltér, mert a Bernoulli-törvény pontos teljesülését sok effektus zavarja: Egyrészt a víz nem tekinthető ideális folyadéknak, így a kiömlőnyílásnál örvények képződnek, s ez csökkenti a vízsugár sebességét, másrészt az egyenletekben a közegellenállással is számolni kell. A pontos számításoknál az sem elhanyagolható, hogy a széles edényben a vízszint süllyed.
            Mindezen zavaró körülmények ellenére a Weisbach-féle kifolyási készülékkel egészen kiválóan igazolható a Torricelli tétel, de ha mérés helyett csak a látványra hagyatkozunk, akkor is nagy élményt jelent ennek az eszköznek a bemutatása a tanuló ifjúság számára.