Frick-féle vízszintesen hajító készülék (beszerzési év: 1863) |
 |
A Frick-féle vízszintesen hajító készülékkel a vízszintes hajítást lehet igen szemléletesen bemutatni. Az eszközzel tökéletesen bemutatható, hogy a vízszintes hajítás felbontható egy vízszintes irányú, egyenes vonalú egyenletes mozgásra, és egy függőleges irányú, gyorsuló mozgásra (szabadesésre). |
A Frick- féle vízszintesen hajító készülék |
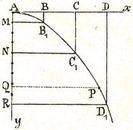
Ha valamely testet vízszintes irányban hajítunk el, tehetetlensége miatt a hajítástól nyert v sebességével az egymásra következő másodpercekben az AB = BC = CD = ... = v utakat futná be. Mivel azonban a nehézségi erő is hat rá, a szabadesés törvényei szerint egyidejűleg esni is fog. Az első másodpercben
távolságot esik, így a test helye a mozgások összetételének törvénye szerint az első másodperc végén B1-ben lesz. Két másodperc alatt a test távolságot zuhan, így a test helye a második másodperc végén C1-ben lesz. A harmadik másodperc végén a test D1 pontban lesz és így tovább. Így végeredményben a test mozgása gyorsuló, a pályája pedig görbe vonalú lesz. |
A vízszintes hajítás, mint összetett mozgás |
A pálya alakját a következőleg határozhatjuk meg. A pálya tetszőleges P pontját a PQ=x és AQ=y vonalak határozzák meg. Az x és az y valójában a P pont vízszintes, illetve függőleges koordinátái a derékszögű Descartes-féle koordinátarendszerben. Ezek a koordináták egyszersmind a vízszintes, illetve a függőleges irányban megtett utakat is megadják, tehát:
illetve
Az, hogy a test a pálya mely pontjában tartózkodik, függ az időtől, de a test pályája az időtől függetlenül mindig ugyanaz marad. A pálya egyenletét megkapjuk, ha az x-re, illetve az y-ra kapott összefüggéseket egybeírjuk, vagyis az első egyenletből kifejezzük az időt, és behelyettesítjük a második egyenletbe. Így a következő egyenletet kapjuk:
vagy más alakban:
Ez az egyenlet a parabola csúcsponti egyenlete (a tengelyek a szokásos megjelöléshez képest fel vannak cserélve). A pálya tehát olyan parabola, amelynek a paramétere:
|