Az ismert tétel szerint valamely mechanikai rendszer akkor van stabilis egyensúlyi helyzetben, ha a helyzeti energiája a lehető legkisebb. A folyadék helyzeti energiájához a felszínnel arányos felületi energiát is hozzá kell számítani, így – ha a molekuláris erők mellett más erők elhanyagolhatóak- a folyadék igyekszik a legkisebb felszínű helyzetet felvenni.
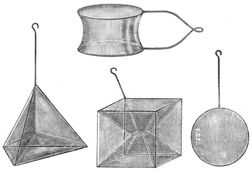
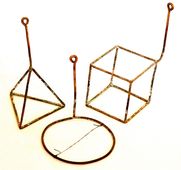
            Ennek a jelenségnek a bemutatására kiválóan alkalmasak azok a híres Plateau-féle sodronyalakok, amelyek a nevüket Joseph Antoine Ferdinand Plateau (1810-1883) belga fizikusról kapták. Ezek a sodronyalakok gyakorlatilag drótból kialakított geometriai formák, amelyeket szappanos vízbe helyezve a drótkereten feszülő szappanhártyák minimálfelületeket, azaz olyan felületeket képeznek, amelyeknek a felszíne a megadott határgörbe mellett a legkisebb.

            A szertárban három különböző Plateau-féle sodronyalak található. Ezek kocka, tetraéder és kör alakúak. Az első két formánál rögtön kiválóan láthatók a minimálfelületek, míg a kör alakú drótváznál a kör kerületének két pontjához kötött laza cérna mindaddig laza marad, míg a cérna mindkét oldalán feszül szappanhártya. Ha a cérna egyik oldaláról eltávolítjuk a szappanhártyát, akkor a cérna kör alakban megfeszül, azaz a maradék hártya szintén igyekszik a legkisebb felületű hártyát elfoglalni.