1. Feladat:  t= 24 h
                 m= 2 kg
                 T₁= 60°C
                 T₂= 100°C
  c_víz= 4,2 kJ/kg°C
  L_f = 2260 kJ/kg
  Q_össz= ?
Az m= 2 kg tömegű T₁= 100°C hőmérsékletű vízgőz lecsapódásakor létrejött energiaváltozás:
 Q₁=L_f ^.m=2260 kJ/kg^.2 kg= 4520 kJ .
Az m=2 kg tömegű T₁= 100°C hőmérsékletű víz T₂=60°C hőmérsékletűre való lehűlésekor bekövetkező energiaváltozás:
               Q₂= c_víz^.m^.(T₁- T₂)= 4,2 kJ/kg^.°C^.2 kg^.40°C= 336 kJ .
Az összes energiaváltozás 1 óra alatt:
               Q= Q₁+Q₂=4520 kJ+336 kJ= 4856 kJ .
Az összes energiaváltozás 24 óra alatt:
  Q_össz=24^.4856 kJ= 116544 kJ .

Tehát a radiátor környezetének energiaváltozása egy nap alatt: 116544 kJ .

 
2.Feladat:
 _test= 4 kg/dm³= 4000 kg/m³
 _víz= 1000 kg/m³
  F_tartó= 12 N
  g= 10 N/kg
  V_test= ?
   m_test= ?

a.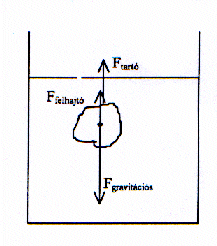

A rajz alapján felírhatjuk az egyensúly feltételét:                   Ftartó+Ffehajtó= Fgravitációs  Azaz:                   Ftartó+víz.g.Vtest=mtest.g                   Ftartó+víz.g.Vtest=test.Vtest.g                   12 N+1000 kg/m3.10 N/kg.Vtest= 4000 kg/m3. Vtest.10 N/kg  Ebből adódik, hogy Vtest= 0,0004 m3=0,4 dm3 .

b. A test tömege: m_test= _test^.V_test= 4000 kg/m^3.0,0004 m³= 1,6 kg .

Tehát a test térfogata  0,4 dm³, a test tömege  1,6 kg .

3.Feladat: R= 4 
                  U= 3 V
                  I_telep= ?
a. Az ábra alapján látszik, hogy egy R₁=1/4^.R =1és egy R₂= 3/4^.R= 3  ellenállású huzaldarabot párhuzamosan kötöttünk.
( Mivel a huzaldarabok ellenállásai egyenesen arányosak a hosszukkal.)
Így az áramkör eredő ellenállása:
   = + 
 
  =  +    R_eredő= 3/4 

Ebből Ohm törvényét felhasználva adódik a telepen átfolyó áram erőssége:
 
 I = =  = 4 A .
Tehát a telepen átfolyó áram erőssége 4 A .

b. Ha azt szeretnénk, hogy a a telepen átfolyó áram erőssége felére csökkenjen akkor a kör ellenállását kétszer akkorára kell
 növelnünk. Így a második kérdésre a válasz :
Az áramkörbe egy R’= 3/4 -os ellenállást kell bekötni még a B és a C pontok közé.
 

Totó: 1x2  12x  x2x  1221  2