1.Feladat: s=780 m
                  t₁=50 s
                  t₂=11 s
                  t₃=55 s
                  L=?
                  v=?
                  v_motor=?
a. A vonatnak t₂ idő alatt kell megtennie a saját hosszát, valamint t₁ idő alatt megteszi a saját hosszának és az alagút hosszának az összegét: L/t₂ = (s+L)/t₁, azaz L/11=(780+L)/50
Az egyenletet megoldva L=220 m adódik.
Tehát a vonat hossza: 220 m.
b. Ezek után adódik a sebesség: v = L/t₂ = 220 m/11s = 20 m/s.
Tehát a vonat sebessége 20m/s.
c. Itt két megoldás adódik:
I. Ha a motoros gyorsabb a vonatnál, akkor a motorosnak t₃ idő alatt meg kell tennie a vonat által ezalatt megtett utat valamint a vonat hosszát.
Ezért a motoros sebessége: v_motor = (v^.t₃+L)/t₃ = (1100 m+220 m)/55 s = 24 m/s.
Tehát a motoros sebessége 24 m/s.
II. Ha a vonat gyorsabb a motorosnál, akkor a vonatnak t₃ idő alatt meg kell tennie a motoros által ezalatt megtett utat valamint a saját hosszát.
Ezért írhatjuk: v_vonat^.t₃ = v_motor^.t₃+L , így  v_motor^.55s+220 m = 20 m/s^.55s.
Ebből a motoros sebessége 16 m/s.

2. Feladat: P=600 W
                  m₁=0,5 kg
                  T₁= T₂=15°C
                  V₂=2 dm³ víz, azaz m₂=2 kg.
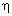                 =0,8
                  c_víz =4,2 kJ/kg^.°C=4200 J/kg^.°C
                  c_al=0,9 kJ/kg^.°C=900 J/kg^.°C
                  L_f=2260 kJ/kg=2,26^.10⁶ J/kg
                  t=?
Felírhatjuk az energiamegmaradás törvényét:
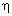^.P^.t= c_al^.m₁^.(T_f-T₁)+ c_víz^.m₂^.(T_f-T₂)+L_f^.m₂
Az egyenletet megoldva azt kapjuk, hogy t=10983,8 s=3,051 h.
Tehát kb. 3 óra múlva fogy el az összes víz a lábasból.

3. Feladat: R₁=2
P=100 W
U=40 V
R=?
Először számítsuk ki a kicserélés uán a teljesítményt:
P₂=U²/5+ U²/2 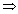  P₂=1120 W .
Ezután kiszámíthatjuk az eredeti teljesítményt:
P₁=P₂-P=1120 W-100 W=1020 W .
Ezt felhasználva, írjuk fel ekkor a teljesítményt:
1020 W=(40 V)²/5+(40 V)²/R 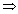  R=2,285 .
Tehát a keresett ellenállás értéke 2,285 .
 

Totó: 1x2  12x  x2x  1221  2