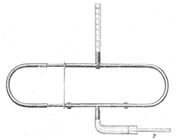
Quincke-féle interferenciacső (beszerzési év: 1904) |
A hangsebesség közvetett mérési módszereinek egy része a hang hullámhosszának a mérésén és a összefüggésen alapszik. Ezen mérések közül az egyik leghíresebb az a kísérlet, amellyel 1866-ban Heinrich Quincke (1842-1922) német fizikus mérte meg a hangsebességet. Quincke a méréséhez egy olyan kettős U alakú, széthúzható csövet használt, amelynek mindkét oldalán egy-egy nyílás (A és B) van elhelyezve. Ez volt az ún. Quincke-féle interferenciacső. |
|
Quincke-féle interferenciacső |
|
A cső egyik nyílásához (A) egy ismert ν frekvenciájú hangforrást (pl. egy hangvillát vagy elektromos hanggenerátort) helyezünk, és a hangot a másik nyílásnál (B) hallgatjuk (vagy ehhez a nyíláshoz valamilyen hangjelző készüléket, pl. érzékeny lángot helyezünk). A B nyílásnál a hang intenzitása a vizsgálandó gázzal megtöltött cső egyik, illetve másik ágában haladó, majd újra találkozó hullámok útkülönbségétől függ. Az alaphelyzetben a két ág egyenlő hosszú, az útkülönbség zérus, a hangintenzitás maximális. Az első hangminimumot, majd a továbbiakat rendre olyan d távolságokkal való széthúzásoknál kapjuk, amelyeknél a 2d útkülönbségek a félhullámhossz páratlan számú többszörösei: 2d = λ62, 3λ/2 stb. Ily módon a hullámhossz (λ) könnyen meghatározható, és a frekvencia (ν) ismeretében az adott közegbeli hangsebesség (c) kiszámítható. |
|