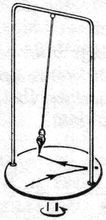
Foucault inga és centrifugálgépre szerelhető „golyóváz”-modell (beszerzési év: 1873-74, illetve 1898) |
 |
|
Az inga egyedülálló a maga nemében. Iskolánk 112 éves „új” épületében a tervező, Sándy Gyula - feltehetőleg az akkori fizikatanárok kérésére- a fizika előkészítő mennyezetébe építette be az inga felfüggesztő szerkezetét, így az gyakorlatilag 110 éve az épület része. Ez ráadásul akkor még viszonylag friss tudományos eredmény is volt, ugyanis Jean-Bernard-Léon Foucault (1819-1858) francia fizikus 1851-ben végezte el történelmi kísérletét. Az idők során a felfüggesztő szerkezet elmozdítható része eltűnt, de az épület centenáriumra, 1996-ra pótoltuk. A megoldás nem lett tökéletes, de azért mutatja az effektust. Hosszú idő után azonban gondos indítás esetén is „beköröz”, és kúpinga-szerűen kezd viselkedni. |
|
Foucault- inga |
|
A híres Foucault-féle kísérlet hátterében az a fizikai jelenség húzódik, hogy a lengő inga, tehetetlensége miatt megtartja lengési síkját. Erről könnyen meggyőződhetünk, ha vékony szálra ólomgolyócskát kötünk, és ezt az ingát valamely állványra felfüggesztjük. A meglendített inga a lengési síkját az állványnak egy függőleges tengely körül való elfordításánál is változatlanul megtartja. Ezt a jelenséget mutatja be az a „golyóváz” modell, amely az 1873-74-es tanévben, a centrifugálgép tartozékaként került a szertárba. |
|
A Foucault inga „golyóváz” modellje |
|
Az egyenlítőnél - ahol a hosszúsági körök, illetve azok érintői párhuzamosak egymással - semmilyen eltérést nem lehet észrevenni a Föld és az inga elfordulása között. Egy tetszés szerinti szélességi körnél azonban a kísérlet úgy jelentkezik, hogy az inga látszólagos elfordulása kisebb, mint a Földnek a megfelelő elfordulása |
|
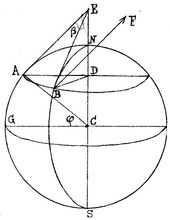
A Foucault-inga periódusidejének magyarázata |
|
Legyen NS a Föld tengelye és jelöljük A-val az észlelőhelyet, amely az ACG=
Mivel az AED szög = ACG szög = A kísérletekből kiderült, hogy az inga látszólagos elfordulása pontosan megfelel ennek a képletnek, ami a Föld tengely körüli forgását kétségtelenül bizonyítja. |
|