|
James Clerk Maxwell (1831-1879) skót fizikus elmélete (1865) – amely szerint elektromágneses hullámoknak kell létezniük, és a fény is elektromágneses hullám– adta az indítékot Heinrich Rudolf Hertz (1854-1894) német fizikus számára, hogy kísérletileg is bebizonyítsa a vákuumban fénysebességgel terjedő elektromágneses hullámok (Hertz-hullámok) létezését, valamint az elektromágneses hullámok és a fényhullámok azonos természetét. Ehhez Hertznek ki kellett mutatnia, hogy mindkét hullám mutatja a visszaverődés, a törés, az interferencia és a polarizáció jelenségét. |
|
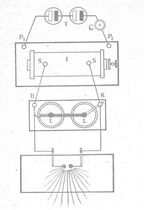
A Hertz-féle oszcillátor bekötési rajza |
Hertz alapvető jelentőségű kísérleteiben (1887) az elektromágneses rezgések, illetve hullámok előállítására egy nyitott lineáris oszcillátor – egy dipólus– szolgált, amely lényegében két, - egymástól kicsiny szikraközzel elválasztott- azonos fémpálcából áll. A áramkörbe való bekötéskor a Ruhmkorff-féle szikrainduktor szekunder tekercsére kötjük egy leydeni-palacknak az egyik, illetve a másik fegyverzetét. Ennek a leydeni-palacknak a külső, illetve belső fegyverzetét kötjük össze az oszcillátor parabolatükrének szorítócsavarjaival. Az áramkör bekapcsolásakor a szikrainduktor áramszaggatójának gyors működése folytán a szekunder tekercsben nagyfeszültségű áram indukálódik, amely feltölti a leydeni-palack fegyverzeteit. Innen a töltések az oszcillátor két fémpálcájára tódulnak, s itt a felhalmozott töltések a pálcák közötti levegőréteget heves csattanással törik át. Mielőtt egy-egy szikra kialudna, a pálcák sokszor áttöltődnek, így oszcilláló kisülések, elektromágneses rezgések keletkeznek. Ezek a rezgések a vezetők kicsi kapacitása miatt igen rövid ideig tartanak, s így a létrejövő elektromágneses rezgések igen nagy frekvenciájúak lesznek. A fémpálcák által a környező térbe küldött elektromágneses hullámok alkalmasnak bizonyultak a híres Hertz-féle kísérletek elvégzéséhez. A fenti módon előállított nagyfrekvenciájú rezgéseknek az oszcillátorból a szikrainduktor tekercsébe való visszajutását fojtótekercsekkel akadályozzák meg.
Az elektromágneses rezgések, illetve hullámok kimutatására Hertz különböző alakú rezonátorokat alkalmazott. Közülük a legegyszerűbbet az oszcillátorral megegyező méretű és alakú – rezonanciára beállított dipólus– rezonátor képviseli. Amikor az oszcillátorból kiinduló elektromágneses hullám, illetve annak gyorsan változó elektromos tere eléri a rezonátort, akkor benne nagyfrekvenciájú elektromos kényszerrezgéseket, illetve áramokat gerjeszt, amelynek az intenzitása akkor a legerősebb, ha a rezonátor az elektromos térrel párhuzamosan helyezkedik el. A nagyfrekvenciájú áramok jelenlétéről Hertz a rezonátor közepén lévő kis nyíláson átugró, nagyítóval megfigyelhető szikrák felvillanásából szerzett tudomást. Ennek az egyszerű rezonátornak egy modernebb változata már egy – gyengébb rezgések megfigyelésére is alkalmas- kristálydetektorral és egy érzékeny galvanométerrel, vagy egyszerűen egy villanycsengővel van felszerelve. Az elektromágneses hullámok kimutatására a rezonátor közepén beiktatott kis izzólámpát is alkalmazhatunk. Ez az eljárás különösen azoknál a demonstrációs kísérleteknél eredményes, amelyeknél az oszcillátor és a rezonátor közötti távolság nem nagy, s ily módon a rezonátorban keletkező elektromos rezgések elegendően erősek. |
|
|
Hertz kísérleti elrendezése |
A Hertz-féle elrendezés fő hiányossága, hogy az oszcillátorban a szabadrezgések gyorsan csillapodnak és viszonylag kis teljesítménnyel rendelkeznek. Ezeket a fogyatékosságokat - a későbbiek során– a szikrainduktor helyett alkalmazott, pl. elektroncsöves generátorok már kiküszöbölték. Az ilyen a generátorokkal gyakorlatilag tetszés szerinti teljesítményt és szabályos szinusz hullámokat tudtak már előállítani. |
A fizikaszertárban található Hertz-féle eszközkészlet részei: |
- 1 db parabolikus tükörrel ellátott Hertz-féle oszcillátor (leadó készülék)
Ez az eszköz a fémből készült parabolatükör fókuszvonalába helyezett két fémpálcából áll, amelyeknek egymás felé fordított vége ki van hegyezve. Ha ezekre a fémekre az erre a célra szolgáló szorítócsavarok segítségével egy szikrainduktor szekunder tekercsét kötjük, akkor a két fém között nagyfrekvenciájú elektromos hullámokat kapunk.
|
|
|
Hertz-féle oszcillátor |
- 1 db parabolikus tükörrel ellátott Righi-féle radiátor (leadó készülék)
Augusto Righi (1850-1920) olasz mérnök olyan leadó készüléket fejlesztett ki, amelyben a rezgő kisülés nem a levegőben történik, így ezzel az eszközzel a Hertz-féle oszcillátornál messzebb is el tudott elektromágneses hullámokat juttatni. Ez az eszköz gyakorlatilag a parabola fémtükör gyújtóvonalába elhelyezett keménygumi cső, amelynek belsejében egymáshoz közel, két nagyobb fémgolyó helyezkedik el. A fémgolyók közötti részt vazelinolajjal töltik ki. A keménygumi cső szélein, a nagyobb golyóktól távolabb két kisebb golyó is található, amelyeket a szorítócsavarok segítségével fémes vezetők kötnek a szikrainduktor szekunder tekercséhez. A Ruhmkorff-féle szikrainduktor beindítása után a vazelinolajban indukálódik egy csillapított kisülés. Az induktor szekunder tekercsének minden egyes nyitása és zárása a csillapított rezgések újabb sorozatát hozza létre, amelyről a keménygumi cső közepén elhelyezett kis nyíláson keresztül szabad szemmel is látható szikrák árulkodnak. Mivel az elektromágneses rezgések csak azonnali kisülések következtében jönnek létre, így a gömb felszínének simának kell lennie, hogy elkerüljük az egyenetlenségek által okozott töltésszivárgást. A vazelinolajba merülés kedvez az azonnali kisülés létrejöttének, az elektromágneses hullámok egységesebb kibocsátásának, és megakadályozza a gömbök felszínének a szikrák által okozott kopását. Emiatt a Hertz-féle oszcillátorral szemben, nem kell a gömbök felületeit állandóan tisztítani.
|
|
|
|
|
- 1 db parabolikus tükörrel ellátott Branly-féle koherer (vevő készülék)
Edouard Branly (1844-1940) francia mérnök 1891-ben olyan vevőkészüléket fejlesztette ki, amely már nagyobb távolságokból is képes volt az elektromágneses hullámokat detektálni. Ez az eszköz gyakorlatilag egy fémből készült parabolatükör fókuszvonalába helyezett néhány centiméter hosszú - fémreszelékkel teli- légmentesen lezárt üvegcső, amelynek a szorítócsavarokkal ellátott végeit, a galvánelemet és az érzékeny galvanométert (esetleg villanycsengőt) magába foglaló áramkörbe kapcsoljuk. Kezdetben a galvanométer nem jelez áramot, illetve a csengő kezdetben nem szólal meg, mert az üvegcsőben levő nikkel és ezüst reszelék laza érintkezése folytán nem folyik áram a körben. Ha a kohererre elektromágneses hullám esik, akkor az addig lazán érintkező, apró fémreszelékek jól összetapadnak, az ellenállásuk lecsökken, s így megindul az áram a körben. Ekkor galvanométer kitér, illetve a csengő megszólal. A koherer gyenge megkopogtatása után – amit a körbe bekötött elektromágnes önműködően is elvégezhet-, az eredeti állapotot hozhatjuk vissza. Az áramkörbe beköthetünk Morse-készüléket, így szolgált ez a kísérlet a drótnélküli táviratozás alapjául.
|
|
|
- 1 db villanycsengő az elektromágneses hullámok vételének kimutatására
- 1 db Hertz-féle drótrács az elektromágneses hullámok polarizációjának kimutatására
- 2 db fémlap az elektromágneses hullámok visszaverődésének kimutatására |
A Hertz-féle eszközkészlettel elvégezhető kísérletek: |
I. Az elektromágneses hullámok létezésének kimutatása
Ha az oszcillátort és a rezonátort, azaz az adót és a vevőt egy-egy parabolikus fémtükör fókuszvonalába helyezzük, és a két fémtükröt egymással szembe, párhuzamosan helyezzük el, akkor a leadó szerkezet oszcillátorának működésbe hozatala után megszólal a vevő szerkezet csengője.
|
II. Az elektromágneses hullámok visszaverődésének szemléltetése
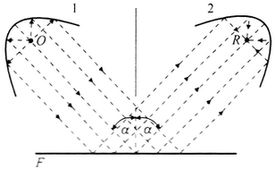
Ha az oszcillátort és a rezonátort, azaz az adót és a vevőt egy-egy parabolikus fémtükör fókuszvonalába helyezzük, akkor - a visszaverődést már tulajdonképpen fel is használva– az oszcillátorral síkhullámnak megfelelő „párhuzamos sugárnyalábot” állítunk elő, amely a rezonátor tükrének gyújtóvonalában koncentrálódik és a rezonátorkörben jól kimutatható áramot kelt. Ha az oszcillátorból kilépő elektromágneses sugarak útjába egy fémlapot helyezünk, akkor a rezonátor helyének megfelelő beállításával bebizonyíthatjuk, hogy itt is érvényes a hullámtanból jól ismert visszaverődés törvénye.
|
|
Az elektromágneses hullámok visszaverődése |
Könnyen meggyőződhetünk arról is, hogy a fémek sokkal jobban reflektálják és abszorbeálják az elektromágneses hullámokat, mint a dielektrikumok. Ha a két fémtükör közé üveg-, ebonit- és más dielektrikum lapot, illetve fémlapot helyezünk el, akkor azt tapasztaljuk, hogy minden dielektrikum jól átengedi az elektromágneses hullámokat, a fémek viszont nem. Ennek a jelenségnek az az oka, hogy a fémek egyrészt erősen visszaverik az elektromágneses hullámokat, másrészt a fémbe behatoló elektromágneses hullámok elektromos tere a fémben áramokat gerjeszt, amelynek energiája Joule-hővé alakul át, úgy hogy az elektromágneses hullám a fémben teljesen abszorbeálódik.
|
III. Az elektromágneses hullámok elhajlásának szemléltetése
Ha az egymással szembe állított oszcillátor és a rezonátor közé egy kb. 1 m2-es fémlapot helyezünk, akkor a fémlap mögé nem tudnak bejutni az elektromágneses hullámok (ún. elektromos árnyék képződik), így a kohererhez bekötött elektromos csengő nem fog jelezni. Ha az elektromos hullámok útjába most egy kisebb fémlemezt helyezünk, akkor a lemez már nem ad éles árnyékot, ilyenkor a hullámok a lemez élein és sarkain elhajlanak. Ennek eredményeként a koherer működésbe jön, s a csengő berregni kezd. Ez a hullámjelenség az elektromágneses hullámok gyakorlati alkalmazásánál alapvető fontosságú, mivel a hullámoknak sokszor nagyméretű akadályokat megkerülve kell elérniük a vevőállomást.
|
IV. Az elektromágneses hullámok polarizációjának szemléltetése
Ha az oszcillátort vagy a rezonátort elforgatjuk az optikai főtengely körül, akkor azt tapasztaljuk, hogy a rezonátorban gerjesztett áram nagysága csökken, és nullává válik, ha az oszcillátor és a rezonátor tengelye egymásra merőleges lesz. Vagyis a rezonátorban fellépő hatás az oszcillátor és rezonátor „párhuzamos állása” mellett maximális, „keresztezett állása” mellett minimális, jeléül annak, hogy az oszcillátor által kibocsátott hullámban az elektromos térerősség vektor iránya az oszcillátorral párhuzamos, azaz a kibocsátott hullám lineárisan poláros.
|
|
|
Hertz-féle rács |
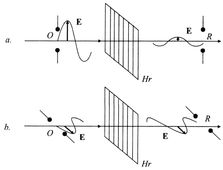
A polarizáció kimutatásának egy másik módja: a párhuzamos helyzetű oszcillátor és rezonátor közé párhuzamos drótokból összeállított rácsot, ún. Hertz-féle rácsot teszünk párhuzamos, majd keresztezett helyzetben. Az első esetben a hullámok nem hatolnak át a rácson, mert az elektromos terük az elektromos térerősség vektor irányával párhuzamos drótokban váltakozó áramot kelt, és emiatt a hullámok elsősorban elnyelődnek a drótokban, melegítik a drótokat vagy a hullámok π fázisugrással visszaverődnek a drótokról, illetve mint antennákból olyan szekunder áramok indulnak ki, amelyek kioltják az áthaladó hullámot. A második esetben viszont a rács hatástalan, azaz átengedi a hullámokat, mert most az elektromos térerősség vektor irányára merőleges drótokban nem jöhetnek létre áramok.
|
|
Az elektromágneses hullámok polarizációja |
V. Az elektromágneses hullámok törésének szemléltetése
Ha az elektromágneses hullámok útjába dielektrikumból (pl. paraffinból, kénből, szurokból) készített prizmát helyezünk, akkor az oszcillátor irányából mérhetjük a prizmára eső beesési szöget, míg a prizmából kilépő elektromágneses hullámok irányát a rezonátor megfelelő mozgatásával tudjuk kellő pontossággal meghatározni. Ezek után a prizma törésmutatójának ismeretében rövid számításokat végezve igazolható a hullámtanból megismert Snellius-Descartes-féle törési törvény.
|
 |
A törés törvénye megnyilvánul pl. egy nagy paraffinból készült lencsének a fókuszáló hatásában is.
|
|
Az elektromágneses hullámok törése |
VI. Az elektromágneses hullámok interferenciájának kimutatása
Ha a leadó és felvevő szerkezetet csaknem egyvonalban állítjuk egymás mellé, és az oszcillátorral szemben elhelyezünk két kicsi fémlemezt, amelyek csak kicsi szöget zárnak be egymással, akkor mindkét fémlapról egyszerre verődnek elektromágneses hullámok a felfogó szerkezet kohererére. Ekkor a kohereren találkozó hullámok erősítik egymást. Ha azonban az egyik fémlapot hátrább toljuk, akkor a rávetődő hullámok hosszabb utat kénytelenek megtenni, mint a helyén maradó tükörre beeső hullámok. Az interferencia eredménye tehát most már a rezgések gyengülésében fog megmutatkozni. Ha az elmozdított lemezt éppen a hullámhossz negyedével visszük hátrébb, akkor a felfogó szerkezetnél találkozó hullámok egymást ki is oltják. Ekkor a csengő csendben marad, ugyanis a két hullám útja között éppen egy fél hullámhossznyi eltérés van. Ezzel az eljárással akár az elektromágneses hullám hullámhosszát is meghatározhatjuk.
|
|
Az elektromágneses hullámok interferenciája |
| |
|
|
|
|
|
| |
|
|
|
|